Representation of arrays in memory

C-style and F-style array transformations are transpose of each other

C-style and F-style non-contiguous layouts are transpose of each other

❶

Indexing in C-style is horizontal while Fortran-style indexing is vertical.

Recall that, a non-contiguous layout with shape (d₀, d₁, …, d_N−1) the value in (n₀, n₁, …, n_N−1) located in the contiguous layout with index n^Style is given by

For C-style		For F-style
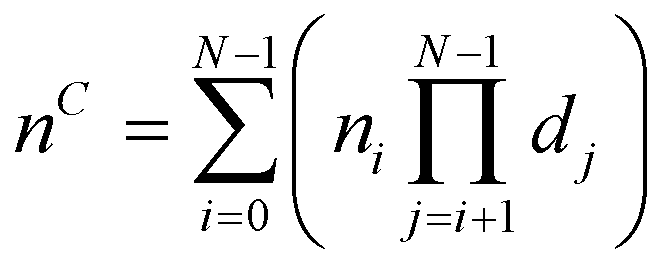
$expression for index in contiguous layout mapped from index in C-style non-contiguous layout$		$expression for index in contiguous layout mapped from index in F-style non-contiguous layout$

such that, for d_k, d_{k + 1}, …, d_m−1, d_m if k > m

$products of d sub j is 1 if start index is greater than final index$

As a consequence, in practice this means that the indexing in C-style is horizontal while indexing in F-style is vertical.

horizontal indexing in C-style and vertical indexing in F-style non-contiguous memory layout

❷

For an index on contiguous layout where are its corresponding indices in C-style and F-style non-contiguous layout?

Let us consider the example of N = 2 dimensional array. Furthermore, let the shape for C-style non-contiguous memory layout be (d₀ = 4, d₁ = 3) and shape for F-style layout be (d₀ = 3, d₁ = 4).

For a given index (n₀ = 2, n₁ = 1) in the C-style non-contiguous layout, its corresponding index in contiguous layout is 7 because

$index in contiguous layout for (2, 1) index in C-style non-contiguous layout is equal to 7$

This index 7 in the contiguous layout corresponds to the index (n₀ = 1, n₁ = 2) in F-style non-contiguous layout because

$index in contiguous layout for (1, 2) index in F-style non-contiguous layout is equal to 7$

word is a compound symbol from (say) a shift register

❸

Similarly, the index 10 in the contiguous layout corresponds to the index (n₀ = 3, n₁ = 1) in C-style since n^C = n₀ d₁ + n₁ 1 = 3 ⋅ 3 + 1 ⋅ 1 = 10 and the index (n₀ = 1, n₃ = 1) in F-style since n^F = n₀ 1 + n₁ d₀ = 1 ⋅ 1 + 3 ⋅ 3 = 10.

Looking at the contiguous layout, moving from index 7 to index 10 requires jumping three elements.

Since, we learned that the contiguous memory layout is mapped from non-contiguous layouts the number of elements that must be jumped from (n₀ = 2, n₁ = 1)^C to (n₀ = 3, n₁ = 1)^C for C-style, and (n₀ = 1, n₁ = 2)^F to (n₀ = 1, n₁ = 3)^F for F-style will also be three elements.

Elements that must be jumped to get from one element to another is the same.

❹